Biologists have the fruit fly. Botanists have the thale cress. Neurologists have the roundworm. These are model organisms: plants and animals that scientists in each of these fields study to make sense of almost all other plants and animals in the world.
For example, in the 1990s, Victor Ambros and Gary Ruvkun discovered a new form of RNA called microRNA (miRNA) in the roundworm Caenorhabditis elegans. For revealing that miRNA regulates genes and allows certain physiological processes in all organisms — including humans — to function properly, Ambros and Ruvkun received the medicine Nobel Prize in 2024.
Similarly, scientists studying recombinant DNA have Escherichia coli, toxicologists have rats, anatomists have zebrafish, those studying hepatitis have rhesus macaques, and so on.
In the same vein, condensed-matter physicists have the Ising model.

A simple, powerful model
The German physicist Ernst Ising created the Ising model in 1924 following a suggestion by his PhD supervisor Wilhelm Lenz. The Ising model provides a simple way to solve problems involving systems where different types of units interact with each other.
For example, say there’s a gas of a few million hydrogen atoms trapped in a chamber and a magnetic field is applied. You need to find out how much the energy of the gas has changed. Since each of these atoms itself is like a tiny magnet and has a north pole (or south pole) pointing in some direction, you can represent it as a grid of atoms:
↑ ↑ ↓ ↑
↑ ↓ ↑ ↑
↓ ↓ ↑ ↓
… where ↑ means ‘north is pointing up’ and ↓ means ‘north is pointing down’. This is a basic instance of the Ising model. You can say that if two neighbouring atoms are ↑↓ or ↓↑ (anti-aligned), it entails an energy of X, and if they’re ↑↑ or ↓↓ (aligned), an energy of Y. This way, you have a simple mathematical way to estimate various values of X and Y throughout the grid and use them to quickly calculate the overall energy.
The Ising model has been used to understand the properties of many solids and liquids in various conditions — including magnetism in metals and alloys and the motion of atoms. Scientists have also used it to simulate land-use change, the flow of opinions in families and religious congregations, and to make sense of neural networks and lay the foundations of modern artificial intelligence (AI). Such work won the US physicist John Hopfield a share of the physics Nobel Prize last year.
Not a two-way street
But for the great applicability and ease of use of the Ising model, there are also many natural systems whose dynamics it doesn’t capture. This is disappointing. One important class of systems is where the direction of effect matters. In the first neural network that Hopfield designed, for example, information could flow in either direction in a connection between two nodes in a network. But in a subsequent version called a feedforward neural network, information could only flow from node A to node B, not from B to A. Such networks were important to build AI models with memory.
A new study published in Physical Review Letters has introduced a new form of the classic Ising model that, by incorporating non-reciprocal interactions, could recreate many properties of one-way networks. As a result, the new model can simulate a larger variety of real-world systems, including social networks, political strategies, and ecological dynamics.
Scientists develop models to understand the simplest set of rules required to explain how a given system works at different scales. “While minimalistic,” the researchers wrote in their paper, the new model “contains features arising in models of the human brain, opinion dynamics, … and micromechanical oscillators”. This means these features’ properties can now be explored using the model.
The researchers are Yael Avni, David Martin, Daniel Seara, and Vincenzo Vitelli of the University of Chicago and Michel Fruchart of ESPCI Paris.

If a system has non-reciprocal interactions, it means the relationship between two components is asymmetric. For example, the way atom A affects atom B won’t be the same way atom B affects atom A. Such interactions are prevalent in the real world, including in neuroscience, ecology, and active matter.
For example, in a hierarchical network like a political party, party members are influenced by the leader’s decision but the leader isn’t affected by the members’ decisions. In biology, the population of a parasite species could affect the well-being of the host but the reverse relationship need not hold. Similarly, power grids often use one-way signals to manage small parts of the network — including to adjust power flow, detect faults, and to send updates between substations. To understand the behaviour of any of these systems, physicists and engineers need models that can anticipate the effects of asymmetric relationships.
Non-reciprocal systems also often display a phenomenon called a limit cycle: as changes propagate within a system, the entire system develops sustained, time-dependent oscillations. Models like the new non-reciprocal Ising model are required to understand how they evolve over time.
Two rules and one condition
In the new study, the researchers developed a non-reciprocal Ising model with two kinds of atoms, P and Q, each of which can be ↑ or ↓. These atoms are arranged on two grids, one in two dimensions and the other in three dimensions. Both grids follow two rules:
(i) Ps next to Ps and Qs next to Qs tend to align. This means that over time Ps and Qs can form islands of uniform alignment.
(ii) If a P is next to a Q, then the P will try to align with the Q (↑ to ↑ or ↓ to ↓). However, a Q next to a P will tend to become anti-aligned with the P (↑ to ↓ or ↓ to ↑). This is the non-reciprocal interaction.
In the reciprocal Ising model, neighbouring atoms being ↑↓ or ↓↑ entailed an energy of X and being ↑↑ or ↓↓ entailed an energy of Y. This meant the overall energy of the system would have been some combination of X and Y. When he created his neural network in the 1980s, John Hopfield set up a similar grid, then gave each node in the grid a condition to follow: whether it was ↑ or ↓ depended on which state made sure the system’s overall energy was lower. By minimising that energy, all the nodes in the network settled down into a given pattern of ↑ and ↓.
Similarly, in the new study, the researchers gave their Ps and Qs a rule to follow. Rather than minimise the overall energy of the grid, each P or Q would have to minimise its own “selfish energy”.
A clock in the grid
The properties of this non-reciprocal Ising model, whatever they are, also tell us about real-world setups that are constructed the same way, e.g. information flowing in political parties and parasites and hosts interacting in an ecosystem. So what did the researchers find?
First, they found that at any given time, the non-reciprocal Ising model could have one of three phases: disordered, where the ↑s and ↓s are all arranged too randomly for there to be an overall ‘order’; ordered, where the ↑s and ↓s have a fixed arrangement that doesn’t keep varying; and the swap phase, where which species has the most order — Ps or Qs — keeps alternating over time, like the tick-tock of a clock.
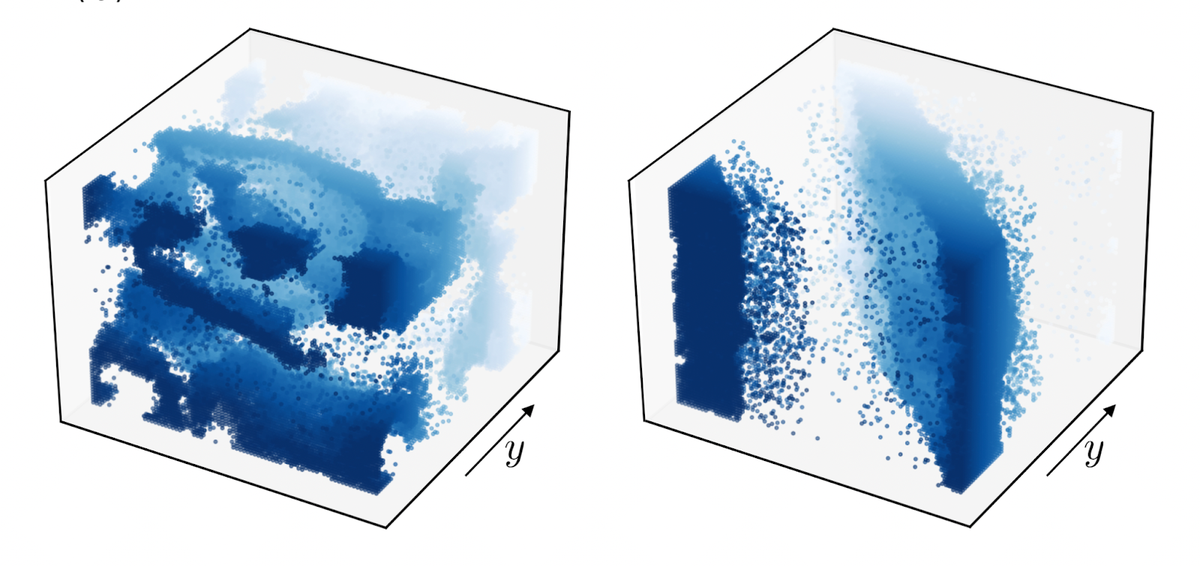
A non-reciprocal Ising model in 3D, shown here in two particular states. The blue dots show ↑↑ states and the shade depicts the depth of dots along the y axis.
| Photo Credit:
arXiv:2409.07481v2
The researchers also found important differences between the 2D and 3D versions of the model. In 2D, both the ordered and the swap phases were suppressed whereas in 3D, the swap phase was able to attain a stable state.
(According to another paper by the same group of researchers published in Physical Review E, the 3D swap phase had the properties of a time crystal. This is wonderfully strange: time crystals are an unusual state of matter in which a material has a stable, oscillating state.)
Finally, the researchers found that if they introduced an asymmetry between Ps and Qs in some form — e.g. the rate at which they flipped from ↑ to ↓ or vice versa — the ordered phase was able to stabilise in the 2D grid.
Wealth of applications
The Ising model and various revisions to it revolutionised the study of condensed-matter physics — often by revealing the simple rules lying at the obscured heart of seemingly complex systems. By extending the Ising model to include non-reciprocal interactions, the researchers behind the new studies have now expanded the model’s usefulness to more domains across scientific fields.
The phase transitions found in the new model may now reveal hitherto unrecognised dynamics in these domains.
The findings also have potential applications in understanding rhythmic activities in biological systems and designing synthetic ‘active materials’ — which take in energy and perform some function, like bacteria swimming in water, starlings murmurating in mesmerising patterns in the sky, and even microscopic robots figuring out which formation to fly in.
Published – May 20, 2025 05:30 am IST

